For the second part of our two-post series, we'll be talking about very special kinds of "moves" in knot theory, with which you can pull and twist a knot around while keeping it as the same knot. These rearrangements, as a whole, which are made without passing the knot through itself, are called isotopies.
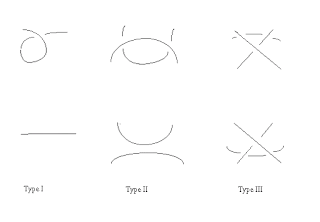
There are three types of moves allowed, called the Reidemeister Moves (see Figure 1). These moves enable us to take away or add a crossing.
Figure 1 - The Reidemeister Moves
The first Reidemeister move allows us to put or remove a twist in the knot (Figure 2),
Figure 2 - This is the first Reidemeister move.
The second Reidemeister move allows us to either add two crossings or remove two crossings from the knot (Figure 3).
Figure 3 - This is the second Reidemeister move.
The third Reidemeister move allows us to slide a strand of a crossing from one side to another of a crossing (see Figure 4).
Figure 4 - This is the third Reidemeister move.
Invariants, which we talked about earlier, are preserved under Reidemeister moves, which is what makes these especially important.
Thanks for reading, and keep up for the next post!
Works Cited:
Adams, Colin Conrad. The Knot Book. New York: W.H. Freeman, 1994. Print.
Armstrong, John. "Reidemeister Moves". The Unapologetic Mathematician. N.p., 2007. Web. 20 Feb. 2016.
Win.tue.nl,. N.p., 2016. Web. 20 Feb. 2016.



These images are really helpful in understanding your project, thanks for providing them!
ReplyDeleteHave you run into any unexpected challenges or surprises so far in your project?
I'm glad the images helped!
ReplyDeleteThanks for asking, though. So far, in my project, I've found that my initial research question was too broad, and, therefore, I am narrowing down my focus, by considering various possibilities through these many invariants.
Thans for using images, it really helps understand. For the first Reidemeister move though, why can I not just pull and wouldn't the knot xome undone (maybe the picture makes it seem easier than it is?)?
ReplyDeleteI'm glad you asked.
DeleteReidemeister moves are applied onto other existing knots to preserve the knot structure and type, essentially. (ie - You take a part of a knot at you twist it like the Reidemeister moves, which is how one is allowed to legally move around the knot.)
Like everyone else, very thankful for the images! What are the applications of Reidemeister moves for you?
ReplyDelete