Tricolorability

Hello!

Thanks for keeping up with the blog, and reading up til now.


Today, we'll be talking about two different invariants - Tricolorability, and Ubercrossings and Petal Number.

We'll begin by explaining tricolorability.

So far, with the Reidemeister moves and all of the other invariants we've been talking about, we claim that these are all distinct knots that we can separate from eachother - with the help of these very invariants that we use.

However, how do we know, in the first place, that these knots are all separate. How do we know that some knot that we deem not to be the unknot cannot have a series of Reidemeister moves through which it can become the unknot?

Tricolorability is a clear invariant because, it's obvious.

Remember what a crossing in a knot is? (Hint - It's the place where one piece crosses over another) We call a crossing an undercrossing for the piece underneath, and an overcrossing for the piece above. In a knot projection, the undercrossing will be the piece that is broken up, and the overcrossing will be the one that is continuous.

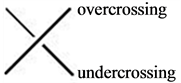Figure 1 - In a crossing, this is the overcrossing and the undercrossing. 

Let us call a strand of a knot the length ranging from one undercrossing to the next.

Now, we can define tricolorability. Do you remember all of those map coloring things where you had to color a map (or just a picture) with 3 or 4 colors? This is similar, in a way.

A knot, or a projection of a knot, is said to be tricolorable if the strands of the knot can be colored so that at every crossing (where 2 or more strands of the knot meet), three different colors or three of the same colors come together. There is, also and interestingly, a rule that a tricolorable knot must be colored with at least two colors.

For example, the trefoil in Figure 2a is obviously tricolorable, but the pretzel knot in Figure 2b would also be tricolorable.

Figure 2a - The trefoil is tricolorable. All of its strands are of three different colors at each of the crossings.

Figure 2b- This is the pretzel knot - note that at every crossing, the colors are either all different or all the same.

Alternatively, though, the figure-8 knot and the unknot are both not tricolorable, the unknot (in Figure 3a) for obvious reasons, and the figure-8 knot (in Figure 3b), because it cannot be colored in three colors.

Figure 3a - The unknot is tricolorable because it can only be colored with one color.

Figure 3b - The Figure-8 knot is uncolorable because it cannot be colored with three colors at one crossing.

This invariants gives us a clear distinction between the unknot and the rest of our knots, which proves knot theory to be non-trivial and is helpful for all the work done in it so far.

How do we show that the Reidemeister moves do not affect the tricolorability of the knot, then?

Well, that'll be in the next post - Reidemeister moves and Tricolorability! Keep on reading for more!